Go2SchooI
Jizx's Personal Page

Cable Driven Manipulator 2 - Kinematics

The kinematics consists of two layers of models, firstly for the transformation relation from joint space to Cartesian space for the overall kinematic properties of the manipulator, and additionally to analyse the transformation relation from drive space to joint space.

Joint space to Cartesian space

Latest kinematics code implementation is in my repository cable_driven_manipulator, including forward kinematics, inverse kinematics, Jacobian matrices, etc.

Version 2.1

Supplement KUKA LBR iiwa manipulator demo, completing inverse kinematics based on gradient projection method (GPM).

Assume \(\theta5\) has max as pi/2 and min as pi/3.

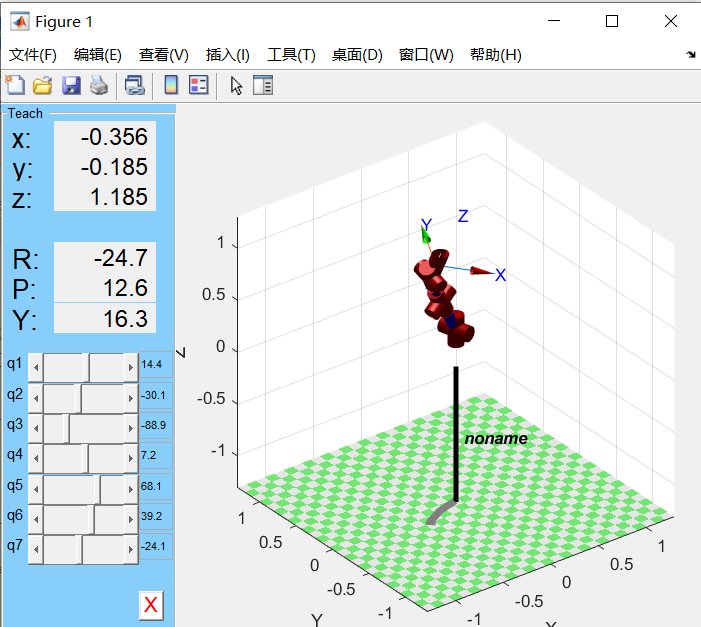
image-20240130201539629

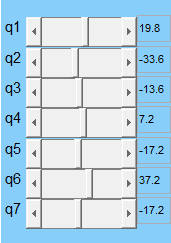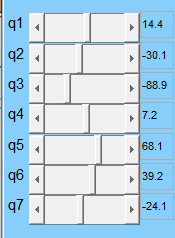target dls_result
Figure 1 Target Angle
Figure 2 Result Angle

We can see that \(\theta5\) is limited.

Version 2.0

Based on the purpose of effect visualisation, function encapsulation other than inverse kinematics is completed.

Add KUKA LBR iiwa manipulator demo, completing inverse kinematics based on Damped Least Square (DLS) method.

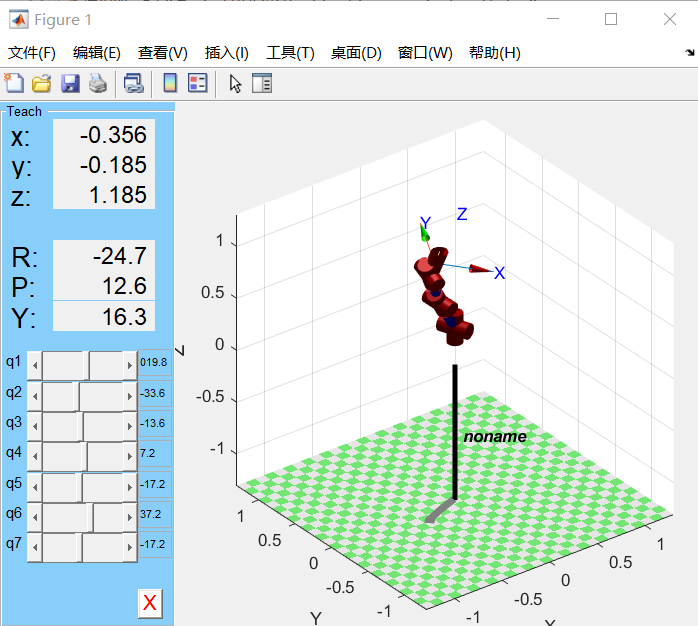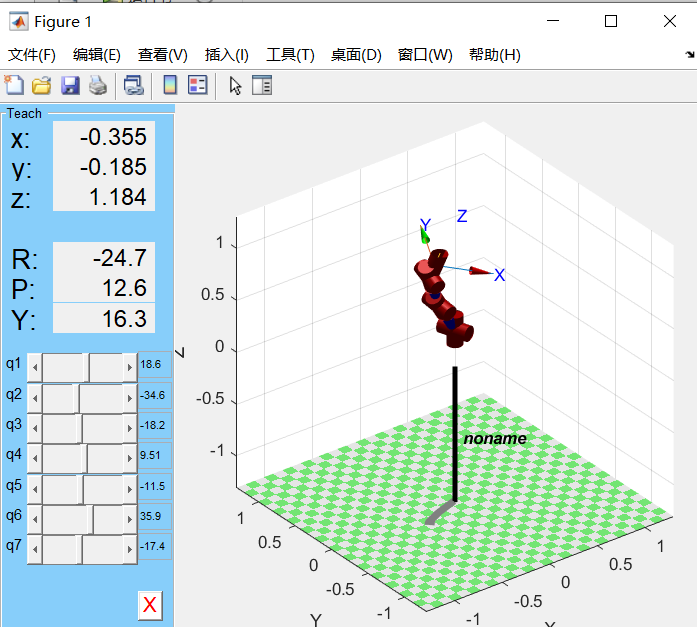target dls_result
Figure 1 Target 6D Pose
Figure 2 Result 6D Pose

Version 1.0

Algorithm validation using PUMA560 as an example:

close all,
clear,clc;

%% Modified DH parameters

L1 =  Link([ 0,    0,       0,        0,      0], 'modified');
L2 =  Link([ 0,    0,      -0.03,      -pi/2,    0], 'modified');
L3 =  Link([ 0,    0,      0.34,       0,      0], 'modified');
L4 =  Link([ 0,    0.338,   -0.04,   -pi/2,    0], 'modified');
L5 =  Link([ 0,    0,      0,        pi/2,    0], 'modified');
L6 =  Link([ 0,    0,      0,       -pi/2,    0], 'modified');
robot_modified = SerialLink([L1,L2,L3,L4,L5,L6]); 
% robot_modified.display();  
robot_modified.teach([0 0 0 0 0 0]);

theta_target = [deg2rad(10.8), deg2rad(-3.6), deg2rad(-3.6), deg2rad(7.2), deg2rad(-7.2), deg2rad(7.2)];

p_target = robot_modified.fkine(theta_target);
q = rad2deg(robot_modified.ikine(p_target));

%% 正运动学手搓好使

% alpha = [0 -pi/2 0 -pi/2 pi/2 -pi/2];
% d = [0 0 0 0.338 0 0];
% a = [0 -0.03 0.34 -0.04 0 0];
% T06 = eye(4);

%     for k = 1:6
%         T_XY_1 = cos(theta(k));
%         T_XY_2 = -sin(theta(k));
%         T_XY_3 = 0;
%         T_XY_4 = a(k);
%         T_XY_5 = sin(theta(k)) * cos(alpha(k));
%         T_XY_6 = cos(theta(k)) * cos(alpha(k));
%         T_XY_7 = -sin(alpha(k));
%         T_XY_8 = -sin(alpha(k)) * d(k);
%         T_XY_9 = sin(theta(k)) * sin(alpha(k));
%         T_XY_10 = cos(theta(k)) * sin(alpha(k));
%         T_XY_11 = cos(alpha(k));
%         T_XY_12 = cos(alpha(k)) * d(k);
% 
%         T_XY = [T_XY_1  T_XY_2  T_XY_3  T_XY_4;
%                 T_XY_5  T_XY_6  T_XY_7  T_XY_8;
%                 T_XY_9  T_XY_10 T_XY_11 T_XY_12;
%                 0       0       0       1];
% 
%         T06 = T06 * T_XY;
%     end

%% 逆运动学中雅可比矩阵求解较为复杂，暂时调用Robotics Toolbox

N = 1000;
x_target = p_target.t';
x_ = zeros(1,3);
e = zeros(1,6);
eplot = zeros(1,N);
theta = [0, 0, 0, 0, 0, 0];

for j = 1 : N
    %平移    
    p = robot_modified.fkine(theta);
    x_(1:3) = p.t';
    e(1:3) = x_target - x_;
    
    %旋转
    Rq = t2r(p);
    rrr = t2r(p_target) * Rq';
    [thn,V] = tr2angvec(t2r(p_target) * Rq');
    e(4:6) = thn * V;
    eplot(j) = e * e';
   
    Jaco = jacob0(robot_modified, theta);
    dq = Jaco' * e';
    dq = 0.1 * dq;

    theta = theta + dq';
end 

thetadeg = rad2deg(theta);
%% 

figure();
plot(eplot)

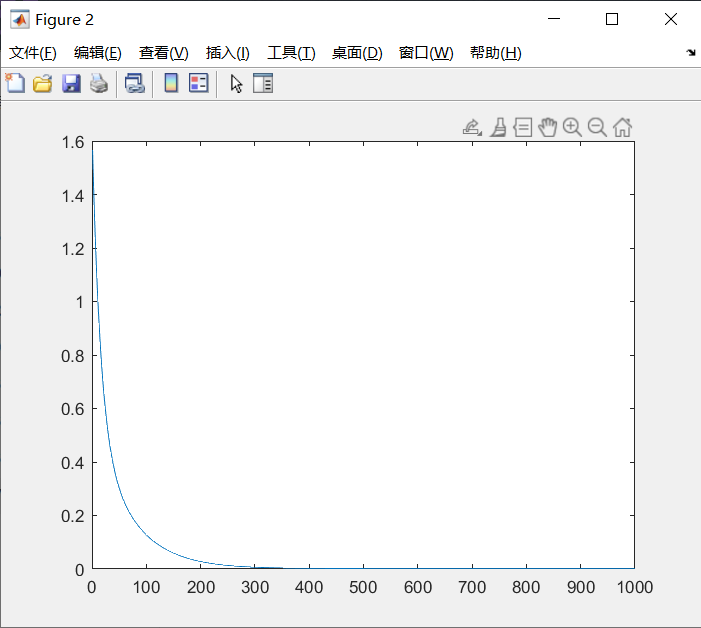
image-20231207152440376

Error design:

e(1:3) is the translation error, which can be calculated from $x_{target} - x$.

e(4:6) is the rotation error, described by the rotation matrix.

Suppose there is a vector called $A_1$ in coordinate system 1, $A_2$ in coordinate system 2, then:

\[A_2=C_1^2A_1\]

For the same reason:

\[A_3=C_2^3 A_2\]

Then

\[A_3=C_2^3 C_1^2 A_1\]

So

\[C_1^3=C_2^3 C_1^2\]

This formula describes the conversion of two rotations added together into one larger rotation. That is, the addition of rotations.

So

\[C_2^{3^{-1}} C_1^3=C_1^2\]

This would indicate that a large rotation minus a small rotation equals another rotation. That is, subtraction between rotations.

In matrix operation, “inverse” is not easy to find, the best matrix to find is “transpose”. But since the rotated matrix is “orthogonal matrix”, its “transpose” = “inverse”, so not only the error of the rotated matrix must be a rotated matrix, but also the calculation process becomes very simple.

\[C_2^{3^{T}} C_1^3=C_1^2\]

References

[1] Peter Corke, MATLAB Robotics Toolbox http://petercorke.com.

[2] SJTU-RoboMaster-Team, Matrix_and_Robotics_on_STM32

[3] J.J.Craig, Introduction to robotics mechanics and control

[4] Buss, S. R. (2004). Introduction to inverse kinematics with Jacobian transpose, pseudoinverse and damped least squares methods. IEEE Journal of Robotics & Automation, 17(1).

[5] Chiaverini, S., Oriolo, G., & Maciejewski, A. A. (2016). Redundant Robots. Cham, Switzerland: Springer.

[6] Woliński, Ł., & Wojtyra, M. (2022). A Novel QP-Based Kinematic Redundancy Resolution Method With Joint Constraints Satisfaction. IEEE Access, 10, 41023-41037. doi: 10.1109/ACCESS.2022.3167403.

Table of Contents